Demystifying Algorithms: A Beginner's Guide to Understanding the Basics

What Are Algorithms?

Algorithms define a procedure for getting a desired output.

You can think of algorithms like a recipe. You follow the steps and you get a desired result (like baking a cake).

When you follow a recipe for baking a cake, you follow the same steps to get the same results each time.

When you run an algorithm, it follows the same steps to get the same output each time.

Still confused? Check out our detailed discussion what is an algorithm.

Why Algorithms Matter?

Algorithms are important in the same way recipes are important...

Efficiency

Algorithms are efficient. Think about baking a cake without the recipe. You may know what you're trying to create, but without the recipe you are left with endless experimentation. Figuring out the different layers, the ingredients, the cooking and preparation time would take a lot longer than just following a simple recipe.

Algorithms are the same way. Without them, computers wouldn't be able to efficiently make decisions or solve problems.

Limited Resources

Baking a cake takes resources. Ingredients are limited. A recipe for baking a cake saves you a lot of resources. Without a recipe, you could waste tons of flour and run out, making it increasingly more expensive to bake your cake!

Like a recipe, algorithms are resourceful. This is important because computers have finite resources. Like the ingredients in your kitchen, the resources available to your computer place limits on what it can do (memory, CPU, storage).

A good algorithm efficiently uses these resources to solve a specific problem. While some algorithms prioritize time or CPU, others prioritize size or memory.

Regardless, an algorithm is judged on it's ability to efficiently solve a problem utilizing the fewest amount of resources.

Fundamental Concepts

Algorithmic Thinking

Like a recipe, algorithmic thinking involves breaking a problem down into smaller parts. By taking a step-by-step approach, you start to think in terms of algorithms that can be implemented in different languages.

Take a problem like finding the largest number in a group. As a human, your brain knows how to innately solve the problem. You quickly scan the numbers and identify the biggest numbers....

But what if you had to explain how to do this? You might say "just look to see what's the biggest number" but that's not how computers work.

For a computer to find the biggest number, it needs a step by step process (back to the recipe analogy).

Considering this, you might start listing out the steps...

1. Sort the numbers from largest to smallest
2. Select the number at the beginning of the list
3. ...

Now you're thinking like a computer. Now your using algorithmic thinking.

Algorithmic Design

Good algorithms run using minimal resources in reasonable time. Algorithmic design speaks to the process of achieving this.

Algorithmic design outlines this process into different steps like

1. Understanding the problem
2. Designing a solution
3. Evaluating the efficiency of the solution
4. Testing the solution
5. Documenting the solution

Remember that algorithms break problems down into smaller steps. Designing the algorithm involves decomposing the problem into different parts first and then defining the steps.

Decomposition is key to algorithmic design.

Algorithmic Complexity

Running algorithms takes time. Running algorithms takes space.

Both time complexity and space complexity are measured to evaluate how efficient an algorithm is.

• Time complexity: How the execution time grows with an increase in input size
• Space complexity: The amount of memory space an algorithm requires concerning its input size.

Both time and space complexity are measured using Big O notation.

Understanding efficiency

Why Efficiency Matters

Efficiency is measured by speed, resource usage, energy consumption, scalability, etc.

1. Without a fast algorithm, things won't get done quickly. (Speed)
2. Without a resourceful algorithm, resource and energy costs increase quickly. (Resource usage)
3. Without an energy efficient algorithm, more energy is consumed more quickly. (Energy consumption)
4. Without a scalable algorithm, a growing input size will make the algorithm less efficient more quickly... (Scalability)

Efficiency matters because without efficient algorithms we don't have efficient finance, health care and everything else relying on algorithms today.

Big O Notation

A good algorithm is an efficient algorithm. Big O notation is how we measure that efficiency.

Using Big O notation, you can compare different algorithms. You can see how their execution time and memory are affected as their input size grows.

This sounds complicated but you can simplify it by envisioning a basic graph...

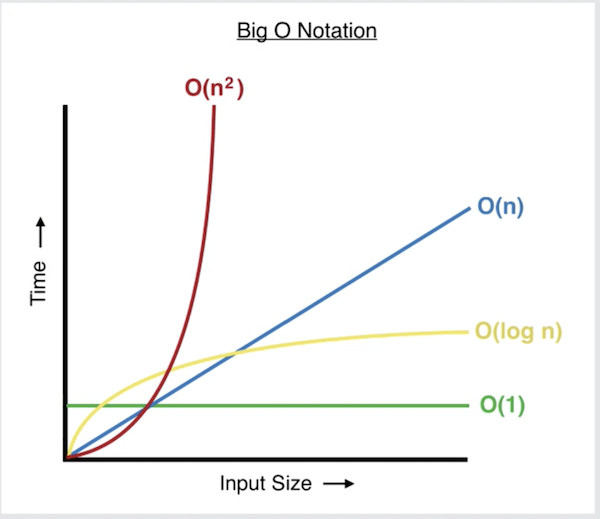
Notice how the X axis is the input size. If your algorithm takes an array as an input, this would represent the size or number of elements in the array.

Notice how the Y axis is the time. This can also represent memory or space used as the input size grows.

Notice how the green line O(1) is a straight line. This represents constant time complexity. The input size has no effect on how long it takes for the algorithm to execute. Accessing an index of an array is a good example of constant time complexity.

Notice how the red line O(n2) exponentially increases in time as the input size grows. This represents quadratic time complexity. This is bad. An example of this would be an function with lots of nested loops.

Common Algorithms

Sorting Algorithms

Sorting algorithms order an array or list of elements based on some comparison.

Here is a basic example of a sorting algorithm in JavaScript...

const sortFn = (arr) => {
    let len = arr.length
    for (let i = 0; i < len - 1; i++) {
        for (let j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                let temp = arr[j]
                arr[j] = arr[j + 1]
                arr[j + 1] = temp
            }
        }
    }
    return arr
}

let arr = [3, 1, 2]
sortFn(arr) //returns [1,2,3]

Notice how this example takes an input array [3,1,2] and sorts it to return the ordered output [1,2,3].

This example is implements a bubble sort. There are many different types of sorting algorithms including merge sort, quick sort, heap sort, etc.

Keep in mind that most programming languages internally implement their own sorting algorithms so you don't have to do all this work. For example, Javascript's Array.sort() method makes it easy to sort array elements without implementing your own sorting algorithms.

Searching Algorithms

Searching algorithms are fundamental to computer science. Database queries, search engines, and information retrieval all rely heavily on efficient searching algorithms.

Linear search

Here's an example of a linear searching algorithm that finds the largest number...

const findLargestNumber = (arr) => {
    let largestNumber
    for (let i = 0; i < arr.length; i++) {
        if (largestNumber) {
            if (arr[i] > largestNumber) {
                largestNumber = arr[i]
            }
        } else {
            largestNumber = arr[i]
        }
    }
    return largestNumber
}

let arr = [1, 3, 2]
findLargestNumber(arr) //returns 3 

This is considered a sequential or linear search algorithm because it checks every element in the array to find the largest number.

This function has linear time complexity (O(n)) or the blue line in the graph above.

Binary search

Here's an example of a binary search algorithm that returns the position of a target value in an array...

function binarySearch(arr, target) {
    let low = 0
    let high = arr.length - 1
    while (low <= high) {
        let mid = Math.floor((low + high) / 2)
        let midValue = arr[mid]
        if (midValue === target) {
            return mid
        } else if (midValue < target) {
            low = mid + 1
        } else {
            high = mid - 1
        }
    }
    return -1
}


let sortedArray = [2, 4, 6, 8, 10, 12, 14]
let targetValue = 10
binarySearch(sortedArray, targetValue) //returns 4

This binary search algorithm only works if the input array is sorted. Notice how the sortedArray argument is a sorted array.

This function has logarithmic time complexity (O(log n)) or the yellow line in the graph above.

The most important part of this article...

So why not just use linear search? You could iterate through the array and return once you find a matching target? Simply iterate and return...?

The answer is efficiency. The binary search approach is much more efficient than a linear search. It instantly saves itself half the work by eliminating half the inputs based on whether or not the mid value is higher/lower than the target.

This may not seem like a big deal, but imagine if the input array had millions of values. Instead of evaluating every element in the array, the binary search keeps reducing the input array by half until it finds what it needs.

This "divide and conquer" approach is a lot more efficient than simply iterating through every single element.

A picture is worth a thousand words. Look at the yellow line in the graph above to see how the execution time levels off as the input size grows. This is MUCH better than the blue line where the time increases as the inputs increase.

Real world applications

Algorithms are fundamental to everything we use computers for! While examples are vast and infinite, here are some common use cases in the real world....

1. Social media: Social media relies heavily on algorithms to populate user feeds. Algorithms are used to determine the best content to show users at the best times and are crucial to recommending connections, friends, etc on social platforms.
2. Finance: Algorithms are used extensively in the finance world to predict trends and execute trades.
3. Forecasting: From predicting the weather to predicting the next words in a sentence (ChatGPT), algorithms are used to evaluate vast amounts of data and forecast outcomes.
4. E-Commerce: Dynamic pricing, product recommendations, etc. are all the result of algorithms.

Tech companies live and die by their ability to implement algorithms. The more efficient an algorithm, the more competitive a solution is to solving a problem.

Algorithms are the life blood of anything driven by technology.

Conclusion

Algorithms are procedures for getting a desired result. You can think of an algorithm like a recipe.

Algorithms are important because they make efficient use of limited resources (memory and CPU).

Algorithms are composed of broken down steps. Designing an algorithm involves breaking down problems into smaller steps and evaluating their efficiency.

Efficiency measures how good an algorithm is. Using Big O notation is the scientific way of measuring this efficiency.

Big O notation evaluates how an algorithm behaves (time, space) as its input size increases.

There are different types of algorithms. Sorting and searching algorithms are prominent examples.

There are many real world examples of algorithms. Anything technology driven relies heavily on algorithms.

Your thoughts?